Si trabajas con conjuntos de datos durante un tiempo suficiente, al final tendrá que tratar con estadística descriptiva. Si le preguntas a una persona común qué es la estadística, probablemente te dirá palabras como «números», «cifras» e «investigación».
Ahora, según los libros, la estadística es la ciencia o una rama de las matemáticas, que consiste en recopilar, clasificar, analizar, interpretar y presentar hechos y datos numéricos. Resulta especialmente útil cuando se trata de poblaciones demasiado numerosas y extensas para realizar mediciones específicas y detalladas. La estadística es crucial para extraer conclusiones generales relativas a un conjunto de datos a partir de una muestra de datos.
La estadística se divide a su vez en dos tipos: descriptiva e inferencial. Aquí revisaremos la estadística descriptiva, incluyendo una definición, los tipos de estadística descriptiva y las diferencias entre estadística descriptiva y estadística inferencial. Algo básico, pero que muchas personas desconocen.
La estadística inferencial gira en modelos matemáticos probabilísticos, y lo revisaré en otro artículo.
Definición de estadística descriptiva
Las estadísticas descriptivas describen, muestran y resumen las características básicas de un conjunto de datos encontrado en un estudio determinado, presentadas en un resumen que describe la muestra de datos y sus mediciones. Ayuda a los analistas a comprender mejor los datos.
Las estadísticas descriptivas representan la muestra de datos disponibles y no incluyen teorías, inferencias, probabilidades o conclusiones. Ése es un trabajo para la estadística inferencial. Este es un punto importante para diferenciar bien lo que es y lo que no es la estadística descriptiva. Veamos más detalles para precisar en que consiste.
Ejemplos de estadística descriptiva
Si quieres un buen ejemplo de estadística descriptiva, no busques más que el promedio de calificaciones de un estudiante. Un promedio de calificaciones reúne los puntos de datos creados a través de una gran selección de calificaciones, clases y exámenes, luego los promedia y presenta una idea general del rendimiento académico medio del estudiante.
Hay que tener en cuenta que el promedio no predice el rendimiento futuro ni presenta ninguna conclusión. En cambio, proporciona un resumen directo del éxito académico de los estudiantes basado en valores extraídos de los datos.
He aquí un ejemplo aún más sencillo. Supongamos un conjunto de datos 2, 3, 4, 5 y 6 equivale a una suma de 20. La media del conjunto de datos es 4, que se obtiene dividiendo la suma por el número de valores (20 dividido por 5 es igual a 4). Es muy simple, pues solo se describe el conjunto de datos.
Los analistas suelen utilizar tablas y gráficos para presentar estadísticas descriptivas. Si a la salida de una sala de cine preguntamos a 50 espectadores si les ha gustado la película que han visto y plasmamos los resultados en un gráfico circular, estaremos hablando de estadística descriptiva. En este ejemplo, las estadísticas descriptivas miden el número de respuestas afirmativas y negativas y muestran a cuántas personas les gustó o no la película. Si intentara llegar a otras conclusiones, se adentraría en el terreno de la estadística inferencial, pero de ese tema publicaré otro artículo más adelante.
Por último, los sondeos políticos se consideran estadísticas descriptivas, siempre que se limiten a presentar hechos concretos (las respuestas de los encuestados), sin extraer conclusiones. Los sondeos son relativamente sencillos: «¿A quién votó como presidente en las recientes elecciones?«.
Tipos de estadísticas descriptivas
Las estadísticas descriptivas se dividen en varios tipos, características o medidas. Algunos autores dicen que hay dos tipos. Otros dicen que tres o incluso cuatro. Puedes revisar estos dos libros de estadísticas recomendados en estos dos enlaces: Libro de Estadística Descriptiva de Montero y aquí: Libro de Estadística descriptiva de Fernández, Sánchez y Largo
Según lo leído y practicado durante mis años de docencia, puedo resumir los tipos de estadísticas en los siguientes.
De Distribución o de frecuencias

Los conjuntos de datos consisten en una distribución de puntuaciones o valores. Los estadísticos utilizan gráficos y tablas para resumir la frecuencia de cada valor posible de una variable, expresada en porcentajes o números. Por ejemplo, si se realizara una encuesta para determinar cuál es el Beatle favorito de la gente, se crearía una columna con todas las variables posibles (John, Paul, George y Ringo) y otra con el número de votos.
Los estadísticos representan las distribuciones de frecuencias en forma de gráfico o de tabla.
Medidas de Tendencia Central
Las medidas de tendencia central estiman la media o centro de un conjunto de datos, hallando el resultado mediante tres métodos: media, moda y mediana.
Media: La media también se conoce como «M» y es el método más común para encontrar promedios. Se obtiene la media sumando todos los valores de respuesta y dividiendo la suma por el número de respuestas, o «N». Por ejemplo, supongamos que alguien intenta averiguar cuántas horas al día duerme a la semana. Entonces, el conjunto de datos serían las entradas de horas (por ejemplo, 6,8,7,10,8,4,9), y la suma de esos valores es 52. Hay siete respuestas, por lo que N=7. Se divide la suma de valores de 52 entre N, o 7, para hallar M, que en este caso es 7,3.
Moda: La moda es simplemente el valor de respuesta más frecuente o que más se repite. Los conjuntos de datos pueden tener cualquier número de modas, incluyendo «cero». Puede encontrar la moda ordenando el conjunto de datos del valor más bajo al más alto y buscando la respuesta más común. Así, usando nuestro estudio del sueño de la última parte: 4,6,7,8,8,9,10. Como puedes ver, la moda es 8.
Mediana: Por último, tenemos la mediana, definida como el valor en el centro preciso del conjunto de datos. Ordena los valores de forma ascendente (como hicimos con la moda) y busca el número que se encuentra en el centro del conjunto. En este caso, la mediana es ocho.
Variabilidad ó Dispersión
La medida de la variabilidad da al estadístico una idea del grado de dispersión de las respuestas. La dispersión tiene tres aspectos: rango, desviación típica y varianza.
Rango: Utilice el rango para determinar la distancia entre los valores más extremos. Empiece restando el valor más bajo del conjunto de datos de su valor más alto. Una vez más, volvemos a nuestro estudio del sueño: 4,6,7,8,8,9,10. Restamos cuatro (el más bajo) de diez (el más alto) y obtenemos seis. Ahí tienes tu rango.
Desviación estándar: Este aspecto requiere un poco más de trabajo. La desviación estándar (s) es la cantidad media de variabilidad del conjunto de datos, que muestra lo lejos que se encuentra cada puntuación de la media. Cuanto mayor sea la desviación estándar, mayor será la variabilidad del conjunto de datos. Siga estos seis pasos:
- Enumera las puntuaciones y sus medias.
- Halla la desviación restando la media de cada puntuación.
- Eleva al cuadrado cada desviación.
- Suma todas las desviaciones al cuadrado.
- Divide la suma de las desviaciones al cuadrado por N-1.
- Halla la raíz cuadrada del resultado.
| Datos | Desviación de la media | Desviación al cuadrado |
|---|---|---|
| 4 | 4-7.3= -3.3 | 10.89 |
| 6 | 6-7.3= -1.3 | 1.69 |
| 7 | 7-7.3= -0.3 | 0.09 |
| 8 | 8-7.3= 0.7 | 0.49 |
| 8 | 8-7.3= 0.7 | 0.49 |
| 9 | 9-7.3=1.7 | 2.89 |
| 10 | 10-7.3= 2.7 | 7.29 |
| M=7.3 | Suma = 0.9 | suma= 23.83 |
Al dividir la suma de las desviaciones al cuadrado por 6 (N-1): 23,83/6, se obtiene 3,971, y la raíz cuadrada de ese resultado es 1,992. Como resultado, ahora sabemos que cada puntuación se desvía de la media una media de 1,992 puntos.
Varianza: La varianza refleja el grado de dispersión del conjunto de datos. Cuanto mayor sea el grado de dispersión de los datos, mayor será la varianza con respecto a la media. La varianza se obtiene elevando al cuadrado la desviación típica. En el ejemplo anterior, elevamos al cuadrado 1,992 y obtenemos 3,971.
Estadística descriptiva univariante
La estadística descriptiva univariante examina sólo una variable cada vez y no compara variables. En cambio, permite al investigador describir variables individuales. Por ello, este tipo de estadística también se conoce como estadística descriptiva. Los patrones identificados en este tipo de datos pueden explicarse utilizando lo siguiente:
- Medidas de tendencia central (media, moda y mediana)
- Dispersión de los datos (desviación típica, varianza, rango, mínimo, máximo y cuartiles) (desviación típica, varianza, rango, mínimo, máximo y cuartiles)
- Tablas de distribución de frecuencias
- Gráficos circulares
- Histogramas de polígonos de frecuencias
- Gráficos de barras
Estadística descriptiva bivariante
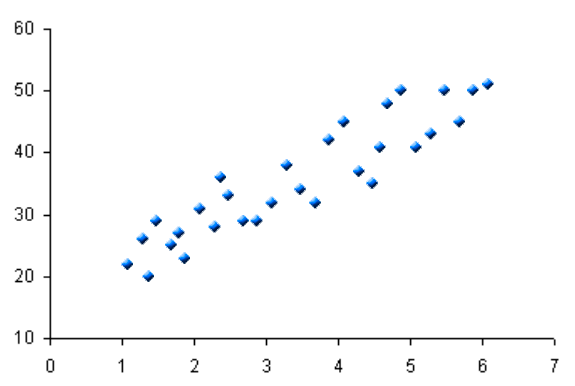
Cuando se utilizan estadísticas descriptivas bivariantes, se analizan (comparan) dos variables simultáneamente para ver si están correlacionadas. Generalmente, por convención, la variable independiente está representada por las columnas, y las filas representan la variable dependiente».
Los datos bivariantes tienen numerosas aplicaciones en el mundo real. Por ejemplo, estimar cuándo se producirá un fenómeno natural es muy valioso. El análisis de datos bivariantes es una herramienta muy útil para el estadístico. A veces, algo tan sencillo como proyectar un parámetro frente a otro en un plano bidimensional permite comprender mejor lo que la información intenta convencernos.
Objetivo principal de la estadística descriptiva
La estadística descriptiva pueden ser útiles para dos cosas:
- Proporcionar información básica sobre las variables de un conjunto de datos y
- Destacar las posibles relaciones entre variables. Los métodos gráficos/pictóricos son medidas de las tres estadísticas descriptivas más comunes que pueden mostrarse gráfica o pictóricamente. Se utilizan para resumir datos.
Las estadísticas descriptivas sólo hacen afirmaciones sobre el conjunto de datos utilizado para calcularlas; nunca van más allá de sus datos. Eso es algo que no debe confundirse y darle atributos de estadística inferencial.








Pingback: Validez y Confiabilidad en instrumentos de Investigación: Claves. - Innovación con Hilmer